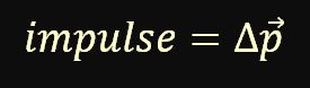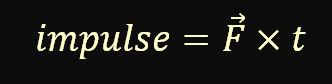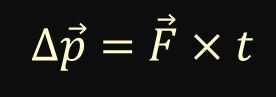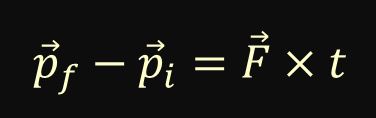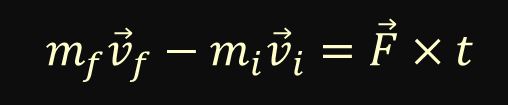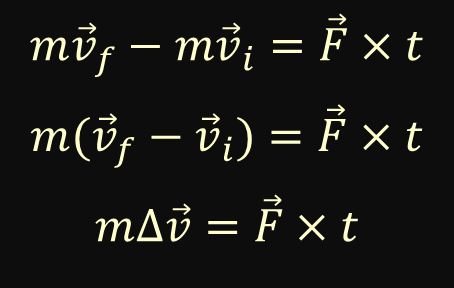Linear Momentum Lab Activity
Page 10 of 12
Impulse has two definitions.
First of all, impulse is defined as change in momentum. When you slow down and stop an egg, you impart an impulse upon the egg because you change its linear momentum.
First of all, impulse is defined as change in momentum. When you slow down and stop an egg, you impart an impulse upon the egg because you change its linear momentum.
As we know, "change in" can be abbreviated as capital Delta, and momentum can be abbreviated as lower-case p with an arrow on top. Thus, we can abbreviate impulse = change in momentum as shown below. In fact, we typically abbreviate impulse as Delta p with an arrow over the p.
Impulse is also defined as force multiplied by time for a constant force. When you slow down and stop an egg, you are able to change its momentum because you exert a force on the egg over some period of time. In fact, the impulse you impart upon the egg is not only equal to the change in momentum of the egg, but the impulse is also equal to the force you exert on the egg multiplied by the time over which the force acts on the egg.
As we know, force can be abbreviated as capital F with an arrow over it, and time can be abbreviated as lower-case t. Thus, we can abbreviate impulse = force multiplied by time as shown below.
Because impulse is equal to both change in momentum and force multiplied by time, for a constant force, we can combine the two impulse equations into the one equation shown below.
We know that change in momentum is equal to final momentum minus initial momentum. Thus, we can re-write the impulse formula as shown below.
We know that momentum is equal to mass multiplied by velocity, and so we can express the impulse formula as shown below.
Because a change in momentum is usually a change in velocity (not a change in mass), we can express the impulse formula as shown below.