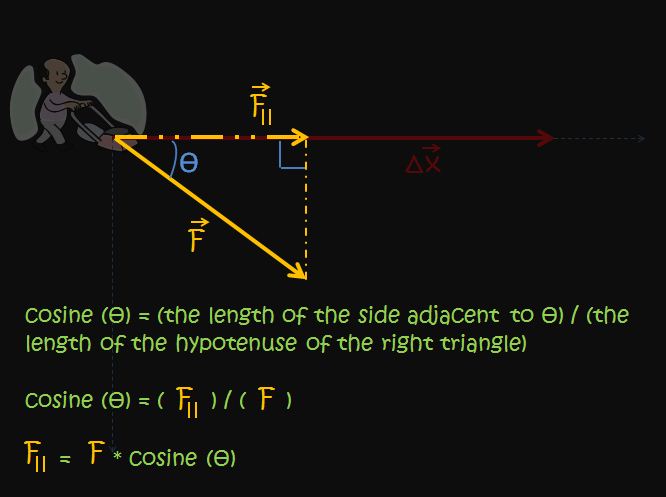
Now, in order to finish finding the magnitude of the component of the man's force along displacement, we must use a tiny bit of trigonometry, but we won't be using anything too difficult. For this example, we need only one trigonometric identity, and it is cosine (theta) is equal to the side adjacent to theta divided by the hypotenuse of the right triangle containing theta.
We've already identified the hypotenuse of our right triangle. In order to use the cosine identity mentioned above, we only need to identify one other side of the right triangle, the side adjacent to theta. The side adjacent to theta is the side which touches theta and which is NOT the hypotenuse. Thus, we can easily identify the side adjacent to theta as the side labeled with a capital F with an arrow over the top and with two short vertical lines as its subscript. In other words, the side adjacent to theta is the component of force which is along the lawnmower's displacement. This is what we need in order to calculate the work done by the man on the lawnmower! The image above shows how to use the cosine identity to find that the magnitude of the component of force along the lawnmower's displacement is equal to the magnitude of the total force exerted by the man multiplied by cosine theta.
Complete the "Cosine Theta Self-Quiz" below to see what you know about the cosine identity.
Cosine Theta Self-Quiz
Complete the crossword, then click on "Check" to check your answer. If you are stuck, you can click on "Hint" to get a free letter. Click on a number in the grid to see the clue or clues for that number.
| 1 | 2 | ||||||||||
| 3 | |||||||||||
| 4 | 5 | ||||||||||
|
|
||||||||||||||